KINETIC THEORY OF GASES
1. Gas Laws
Gas laws are study of any two of quantities like pressure, volume and temperature, when the third is kept constant
A. Boyle's law
- "At constant temperature, the volume of a given mass of gas is invesely propertional to pressure." Thus
V ∝ 1/P
Or, PV = constant (1)
- If P1, V1are initial pressure and volumes and P2, V2be final values then,
P1V1= P2V2
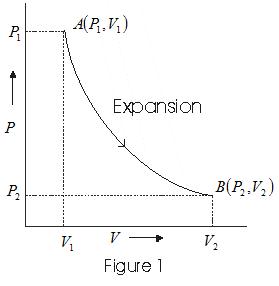
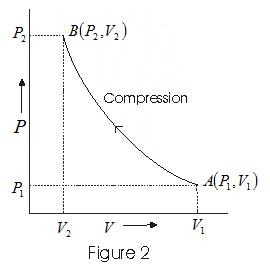
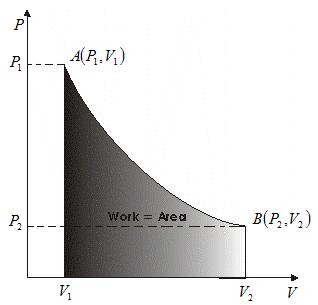
- Graph between P and V at temperature T1 and T2 such that T1<T2 are shown below,
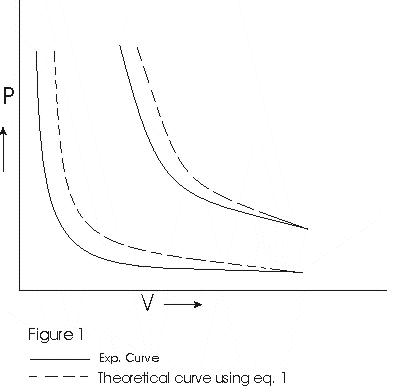
- Graph above shows that Boyle's law is strictly not obeyed by gases at all values of P and T but it obeys this law only at low pressure and high temperature i.e., at law density
B. Charle's Law
- Charle's Law is stated as follows :
"When pressure of a gas is constant the volume of a given mass of gas is directly proportional to its absolute temperature".
V/T = Constant (2)
- Graph between V and T is
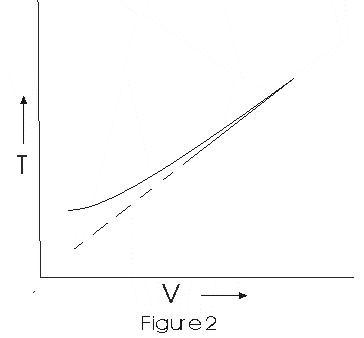
This graph shows that experimental graph deviates from straight line. Theoritical and enperimental graphs are in agreement at high temperature.
2. Ideal gas equation
- We can combine Boyle’s law eqn (1) and charle’s law eqn (2) in to a single eqn i.e.,
PV/T = Constant (3)
If n moles is the mass of gas then we write
PV = nRT (4)
where, n is number of moles of gas, R=NAKB is the universal constant known as gas constant and T is the absolute temperature.
- A gas satisfying eqn (4) at all values of presserves and temperatures is said to be an ideal gas
now no of moles of gas
n = m/M = N/NA
where
m - mass of gas containing N molecules
M - molar mass
NA - Avagadro’s number.
From this,
P = ρRT/M
ρ - mass density of gas.
3. Moleular nature of matter
- We know that molecules which are made up of one or more atoms constitute matter.
- In solids these atoms and molecules are rigidly fixed and space between then is very less of the order of few angestrem and hance they can not move.
- In liquids these atoms and molecules can more enabeling liquids to flow.
- In gases atoms are free to travell without colliding for large distances such that if gases were not enclosed in an enclosure they would disappear.
4. Dalton's law of partial pressures :
- Consider a mixture of non-interacting ideal gases with n1 moles of gas 1,n2 of gas 2 and so on
- Gases are enclosed in an encloser with volume V, temperature T and pressure P.
- Equation of state of mixture
PV = (n1+ n2)RT
or P = n1RT/V + n2RT/V + - - - -
= P1 + P2 + - - --
where,
P1 = n1RT/V
is pressure the gas 1 would exert at same V and T if no other gases were present in the enclosure. This is know as law of partial pressure of the gases.
- The total pressure of mixture of ideal gases is sum of partial pressures of individual gases of which mixture is made of.
5. Kinetic Theory of an ideal gas
Following are the fundamental assumptions of kinetic theory of gases.
- Gas is composed of large number of tiny invisible particles know as molecules
- These molecules are always in state of motion with varying velocities in all possible directions.
- Molecules traverse straight line path between any two collisions
- Size of molecule is infinitely small compared to the average distance traverse by the molecules between any two consecutive collisions.
- The time of collision is negligible as compared with the time taken to traverse the path.
- Molecules exert force on each other except when they collide and all of their molecular energy is kinetic.
- Intermolecular distance in gas is much larger than that of solids and liquids and the molecules of gas are free to move in entire space free to them.
6. Pressure of gas
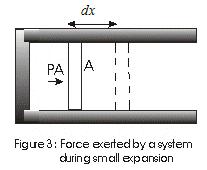
- Consider a cubical vessel with perfectly elastic walls containing large number of molecules say N let l be the dimension of each side of the cubical vessel.
- v1x , v1y, v1z be the x, y, and z componenet of a molecule with velocity v.
- Consider the motion of molecule in the direction perpandicular to the face of cubical vessel.
- Molecule strikes the face A with a velocity v1x and rebounds with the same velocity in the backward direction as the collisions are perfectly elastic.
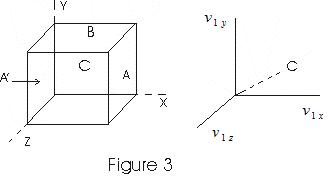
- If m is the mass of molecule, the change in momentum during collision is
mv1x - (-mv1x) = 2 mv1x (1)
- The distance travelled parallel to x-axis an is between A to A´ and when molecule rebounds from A´and travel towards A is 2L
- Time taken by molecule to go to face A´ and then comeback to A is
Δt = 2l/v1x
- Number of impacts of this molecule with A in unit time is
n = I/Δt = v1x/ 2l (2)
Rate of change of momentum is
ΔF = ΔP/Δt
=nΔP
from (1) and (2)
ΔF = mv1x2 / l
this is the force exerted on wall A due to this movecule.
- Force on wall A due to all other molecules
F = Σmv1x2/L (3)
- As all directions are equivalent
Σv1x2=Σv1y2=Σv1z2
Σv1x2= 1/3Σ((v1x)2 + (v1y)2 +( v1z)2 )
= 1/3 Σv12
Thus F = (m/3L) Σv12
- N is total no. of molecules in the container so
F = (mN/3L) (Σ(v1)2/N)
- Pressure is force per unit area so
P = F/L2
=(M/3L3)(Σ(v1)2/N)
where ,M is the total mass of the gas and if ρ is the density of gas then
P=ρΣ(v1)2/3N
since Σ(v1)2/N is the average of squared speeds and is written as vmq2 known as mean square speed
Thus, vrms=√(Σ(v1)2/N) is known as roon mean squared speed rms-speed and vmq2 = (vrms)2
- Pressure thus becomes
P = (1/3)ρvmq2 (4)
or PV = (1/3) Nmvmq2 (5)
from equation (4) rms speed is given as
vrms = √(3P/ρ)
= √(3PV/M) (6)
7. Kinetic interpretation of temperature
- From equation (5) we have
PV = (1/3)Nmvmq2
where N is the number of molecules in the sample. Above equation can also be written as
PV = (2/3)N(1/2)Nmvmq2 (7)
- The quantity (1/2)Nmvmq2 in equation (7) is the kinetic energy of molecules in the gas. Since the internal energy of an ideal gas is purely kinetic we have,
E=(1/2)Nmvmq2 (8)
- Combining equation 7 and 8 we get
PV=(2/3)E
- Comparing this result with the ideal gas equation (equation (4) ) we get
E=(3/2)KBNT
or, E/N=(1/2)mvmq2 =(3/2)KBT (9)
Where, KB is known as Boltzmann constant and its value is KB=1.38 X 10-23 J/K
- From equation (11) we conclude that the average kinetic energy of a gas molecule is directly proportional to the absolute temperature of the gas and is independent of the pressure , volume and nature of the gas.
- Hence average KE per molecule is
(1/2)mv2¯=(3/2)KBT
from this since v2¯=(vrms)2, rms velocity of a molecule is
vrms=√(3KBT/m) (10)
This can also be written as
vrms=√(3KBNT/Nm)
=√(3RT/M) (11)
where, M=mN is the molecular mass of the gas.
Assignment
(1)Gas laws (Boyle's and charle's law) and perfect gas equation can be derived using kinetic theory of gases. try to derive them.
7. Law of Equipartition of energy
- According to the principle of equipartition of energy, each velocity component has, on the average, an associated kinetic energy (1/2)KT.
- The number of velocity components needs to describe the motion of a molecule completely is called the number of degrees of freedom.
- For a mono atomic gas there are three degrees of freedom and the average total KE per molecule for any monotomic gas is 3/2 KBT.
8. Specific Heat Capacity
(i) Monoatomic gases :
- Monoatemic gas moleules has three translational degrees of freedom.
- From law of equipartition of energy average energy of an molecule at temperature T is (3/2)KBT
- Total internal energy of one mole of such gas is
U= (3/2)KBTN
= (3/2) RT (12)
- If CV is melar specific heat at constant volume then
CVv = dU/dT
= (3/2)R (13)
now for an ideal gas
CP - CV = R
CP - molar specific heat capacity at constant presseve
CP = 5/2 R (14)
Thus for a monoatomic gas ratio of specific heats is
γmono = CP/CV= 5/3 (15)
(ii) Diatomic gases :
- A diatomic gas molecule is treated as a rigid rotator like dumb-bell and has 5 degrees of freedom out of which three degrees of freedom are translatoinal and two degrees of freedom are rotational.
- Using law of equipartition of energy the total internal energy of one mole of diatomic gas is
U= (5/2)KBTN
= (5/2) RT (16)
- Specific heats are thus
CV =(5/2)R
γdia= 5/7 (rigid rotater)
- If diatomic molecule is not only rigid but also has an vibrational mode in addition, then
U = (7/2) RT
and CV=(7/2)R
CP=(9/2)R
and γ=CP/CV=9/7
9. Specific heat Capacity of Solids
- From law of equipartation of energy we can can also determine specific heats of solids.
- Consider that atoms in a solid are vibrating about their mean position at some temperature T.
- Oscillation in one dimension has average energy equals 2(1/2)KBT=KBT, as (1/2)KBT is PE and (1/2)KBT is KE of the atom.
- In three dimensions average kinetic energy is 3KBT.
- For one mole of solid total energy is
U= 3NKBT
= 3RT
- At constant pressure ΔQ =ΔU+PΔV=ΔU since for solids ΔV is negligible hence
C=ΔQ/ΔT=ΔU/ΔT=3R
- This is Dulang and Petit law.
- Here we note that predictions of specific heats of solids on the basis of law of equipetation of energy are independent of temperature.
- As we go towards low temperatures T→0 there is a pronounced departure from the value of specific heat of solids as calculated.
- It is seen that specific heats of substance aproaches to zero as T→0.
- This result can further be explained using the principles of quantum mechanics which is beyond our scope.
10. Mean free Path
- On the basis of kinetic theory of gases, it is assumed that the molecules of a gas are continously collilding against each other.
- Molecules move in straight line with constant speeds between two successive collisions.
- Thus path of a single molecule is a series of zig-zag paths of different lengths as shown in fig -.
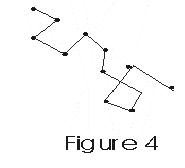
- These paths of different lengths are called free paths of the molecule
- Mean Free Path is the averege distance traversed by molecule between two successive collisions.
- If s is the Total path travelled in Ncoll coilisions, then mean free path
λ= s/Ncoll
Expression for mean free path :
- Consider a gas containing n molecules per unit volume.
- We assume that only one molecule which is under consideration is in motion while all others are at rest.
- If σ is the diameter of each molecule then the moving molecule will collide with all these molecules where centers lie within a distance from its centre as shown in fig
<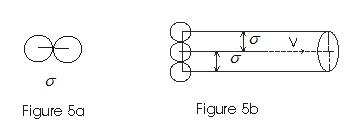
- If v is the velocity of the moving molecule then in one second it will collide with all moleculeswith in a distance σ between the centres.
- In one second it sweeps a volume πσ2v where any other molecule will collide with it.
- If n is the total number of molecules per unit volume, then nπσ2v is number of collisions a molecule suffers in one second.
- If v is the distance traversed by molecule in one second then mean free path is given by
λ = total distance traversed in one second /no. of collision suffered by the molecules
=v/πσ2vn
=1/πσ2n
- This expression was derived with the assumption that all the molecules are at rest except the one which is colliding with the others.
- However this assumption does not represent actual state of affiar.
- More exact statement can be derived considering that all molecules are moving with all possible velocities in all possible directions.
- More exact relation found using distribution law of molecular speeds is
λ=1/(√2)πσ2n
its derivation is beyond our scope.
Solved examples
Question-1.Let A & B are two sample of ideal gases of equal mole .let T be the temperature of both the gas Let EA and EBare there total energy respectively .Let MA and MB are these respective molecular mass .which of these is true
a,EA > EB
b,EA < EB
c,EA =EB
d,none of these
Solution:1
EA = 3/2 nRT
EB = 3/2 nRT
;EA =EB
Question-2. The velocities of the molecules are v, 2v, 3v, 4v & 5v. The rms speed will be
a,11v
b,v(11)1/2
c, v
d, 3.3v
Solution:2
Vrms= (∑ V2 / N)1/2
= [(V2 + 4V2 + 9V2 + 16V2 + 25V2)/5]1/2
=v(11)1/2
Question-3:
An ideal gas A is there.Intial temperature is 27°C.The temperature of the gas is increased to 927°C.Find the ratio of final Vrmsto the initial Vrms
Solution-9:
Vrms=√3RT/M
So it is proportional to Temperature
Now
T1=27°C =300K
T2=927°C =1200K
So intial Vrms=k√300
Final Vrms=k√1200
ratio of final to intial=2:1
Question-.4 Two absolute scales A and B have triple points of water defined as 200A and 350A. what is the relation between TA and TB
Solution-4
Given that on absolute scale
Triple point of water on scale A = 200 A
Triple point of water on scale B = 350 B
Also, triple point of water on Kelvin scale = 273.16 K
Now temperature on scale A and on scale B is equivalent to 273.16 K on absolute temperature scale.
Thus, value of one degree on absolute scale A = (273.16/200) K
Or,
Value of temperature TA on absolute scale A = (273.16XTA)/200
Similarly value of temperature TB on absolute scale B = (273.16XTB)/350
Since TA and TB represent the same temperature
273.16×TA/200 = 273.16×TB/350
Or, TA = 200TB/350 = 4TB/ 7
Question-.5 . which one is not the assumption in kinetic theory of gases
a.the molecules of the gas are in continual random motion
b. The molecules interact during the collison
c. The molecules are tiny hard sphere undergoing inelastic collision
d. The collison are of short duration
Solution-5
Answer is c
Question-.6.
There are two statement
A. Equal volumes of all gases at the same temperature T and pressure P contain an equal no of Molecules
B.the no of molecules in one mole of any gas is 6.0255 * 1022.
which one of the following is correct
a. A and B both
b. A only
c B only
d. A and B both are incorrect
Solution-6
Answer is b
Question-.7. .There are two statement about Ideal gases
A. The Vrms of gas molecules depends on the mass of the gas molecule and the temperature
B. The Vrms is same for all the gases at the same temperature
which one of the following is correct
a. A and B both
b. A only
c B only
d. A and B both are incorrect
Solution-7
Answer is b
Question-.8. .Choose the correct statement of the following
a. The pressure of the gas is equal to the total kinetic energy of the molecules in a unit volume of the gas
b. The product of pressure and volume of the gas is always constant
c. The average kinetic energy of molecule of the gas is proportional to its absolute temperature
d. The average kinetic energy of molecule of the gas is proportional to the square root of its absolute temperature
Solution-8
Answer is c
Question-.9...which one is true according Vander Waal gas equation
a. The attractive forces between the molecules is not negligible
b Volume of the molecules is negligible as compared to the volume occupied by the gas
c. Volume of the molecules is not negligible as compared to the volume occupied by the gas
d. The attractive forces between the molecules is negligible
Solution-9
Answer is a,c